Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure.

 

Case Study Questions

Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure.

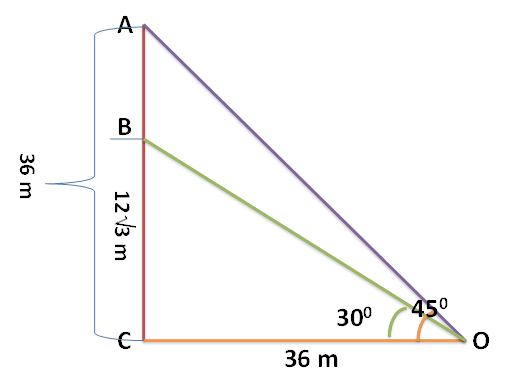
On a similar concept, a radio station tower was built in two stations A and B (B vertically below A). The tower is supported by wires AO and BO from a point O on the ground. Distance between the base C of the tower and the point O is 36 m. From O, the angles of  elevation of the tops of station B and station A are 30º and 45º respectively.

Based on the above, answer the following questions :

(i) Find the height of station B.

(ii) Find the height of station A.

(iii) Find the length of the wire OA.

(iv) Find the length of the wire OB. (CBSE 2022 Set 2)

Solution:

Look at the figure, which we construct now

(i)  Find the Height of  station B

So, we need to find the length of BC

We can take tan O

Tan 30⁰ =

We know the value of tan 30 is 1/Ö3.  Substitute the values

        Cross multiply, we get

        BC =  =  = 12Ö3 m

Hence the length of tower B is 12Ö3 m.

(ii) Find the height of the station A

Here we want to find the length of AC.

CO is known and the angle is 45⁰.  So we take tan 45

Tan 45⁰    =

tan 45⁰     =

We know that tan45⁰ = 1, so substitute the values

        1       =

        AC = 36 m

Hence the height of tower A is 36 m.

(iii)  Find the length of OA

OA is the hypotenuse of the triangle AOC.

Here we know that the length of CO is 36 m and length of AC is also 36 m.

Here we take sin 45⁰.

i.e.,

We know that sin45⁰ = 1/Ö2.  Substitute the values

       

Cross multiply, we get

        AO = 36Ö2 m

Hence the length of the wire AO is 36Ö2 m.

(iv)  Find the length of the wire OB

Consider the triangle BCO.  Here BC and

OC are known and we want to find OB.  In this case we take cos 30⁰ .

        Cos 30⁰ =

We know that cost 30⁰  = .  Substitute the values, we get

       

Cross multiply we get,

        BO =  =  = 12 x 2 x Ö3

        BO = 24 Ö3 m

Hence the length of the wire BO is 24Ö3 m

Summary of Answers:

(i) Height of station B = 12Ö3 m

(ii) Height of station A  = 36 m

(iii) Length of the wire OA = 36Ö2 m

(iv) Length of the wire OB = 24Ö3 m

 

A road roller is a compactor-type engineering vehicle, used to compact soil, gravel, concrete, etc, in the construction of roads and foundations. They are also used at landfills or in agriculture. A company started making road rollers 10 years ago and increased its production uniformly by a fixed number every year. The company produces 800 rollers in the 6th year and 1130 rollers in the 9th year.

 

A road roller is a compactor-type engineering vehicle, used to compact soil, gravel, concrete, etc, in the construction of roads and foundations. They are also used at landfills or in agriculture. A company started making road rollers 10 years ago and increased its production uniformly by a fixed number every year. The company produces 800 rollers in the 6th year and 1130 rollers in the 9th year.

Based on the above information, answer the following questions :

(i) What is the company’s production in the first year ?

(ii) What was the increase in the company’s production every year ?

(iii) What was the company’s production in the 8^th year ?

(iv) What was the company’s total production in the first 6 years ?

Solution:

We can solve this problem with Arithmetic Sequence.

Let, ‘a’ be the production in the first year

And

        ‘d’ be the annual increase in in the production

Given that

        Production in 6^th year = 800 units.

        We know that a_n = a + (n-1)d

Substitute the values, we get

        a + (6-1)d = 800

i.e.,   a + 5d = 800

(or)   a + 5d – 800      (1)

This is the first system of equation.

According to the next condition,

Production in the 9^th year = 1130

i.e.,   a + (9 – 1)d = 1130

i.e.,   a + 8d = 1130

(or)  a + 8d – 1130            (2)

This is the second system of equations

We have to solve these system of equations

        a + 5d – 800 and

        a + 8d – 1130

Subtract the first equation from the second equation

We get,

        (a + 8d) – (a + 5d ) = 1130 - 800

        3d  = 330

        d  = 110

Substitute the value of d back into the first equation

We get,

        a + 5 x 110 = 800

        a + 550 = 800

        a = 800 – 550 = 250.

(i)                  Hence the production in the first year  a = 250 units

(ii)                 The increase in the company’s production in every year
d= 110

(iii)                Company’s production in the 8^th year:\

We know that,

        a = 250 and

        d = 110

So,    a_n = a + (n – 1) d

        a₈ = 250 + (8 – 1) x 110

            = 250 + 7 x 110

            = 250 + 770

           =  1020 units

Hence the company’s production in the 8^th year = 1020 units

iv)  The company’s total production in the first 6 years

        Here we need to find the sum of production,

        We know that,

                Sum = (n/2) x (first term + last term)

                First term = a = 250

                Last term = a₆ = a + 5d = 250 + 5 x 110 = 800

                n = 6

                Sum = (6/2) x (250 + 800)

                        =  3 x 1050

                        = 3150 units

The Final Answer is:

(i)                  The company’s production in the first year is 250 rollers.

(ii)                 The increase in the company’s production every year is 110 rollers.

(iii)                The company’s production in the 8^th year is 1020 rollers

(iv)               The company’s total production in the first 6 years in 3150 rollers.

 

 

 

 

 

Pookalam is the flower bed or flower pattern designed during Onam in Kerala. It is similar as Rangoli in North India and Kolam in Tamil Nadu

 

Case Study 13

Pookalam is the flower bed or flower pattern designed during Onam in Kerala. It is similar as Rangoli in North India and Kolam in Tamil Nadu.

During the festival of Onam , your school is planning to conduct a Pookalam competition. Your friend who is a partner in competition, suggests two designs given below.

Observe these carefully

 

Design I: This design is made with a circle of radius 32cm leaving equilateral triangle ABC in the middle as shown in the given figure.

Design II: This Pookalam is made with 9 circular design each of radius 7cm.

Refer Design I:

1.  Find the side of equilateral triangle.

2.  Find the altitude of the equilateral triangle.

Refer Design II:

3.  Find the area of square.

4.  Find the Area of each circular design.

5.  Find the Area of the remaining portion of the square ABCD.

 

Solution

Refer Design I:

1.     Find the side of equilateral triangle

Look at the figure,

Here O is the centre of the circle

AB, BC and AC are the vertices of the triangle.

Given that D ABC is Equilateral triangle

i.e., AB = BC = AC.

Given that radius is 32 cm

i.e., OB = OC = OA = 32 cm

Now, Let us consider D OBC

Draw a line OM perpendicular to BC

i.e, OM ^ BC

Therefore, ÐOMB = 90⁰

Also

          BM = MC = ½ BC

          ÐBOM = ÐCOM = ½ ÐBOC

                             = ½ x 120

                             = 60⁰.

In right angled triangle OBM 

          Sin O =

          Sin 60⁰ =

            =

          BM =  = 16 Ö3 cm

Thus

          BC     = 2 x BM

                   = 2 x 16 Ö3

                   = 32 Ö3 cm

Hence the side of the equilateral triangle is 32 Ö3 cm.        

(ii) Find the altitude of the equilateral triangle

Draw the attitude AM perpendicular to BC

AM    = AO + OM

          =  32 + OM

Now find the OM

Consider the triangle BOM 

          Find Cos O

Cos O =

Cos 60⁰ =

½ =

OM =  cm

Therefore,

Attitude of equilateral triangle ABC = 16 + 32 = 48 cm

 

Refer Design II:

1.  Find the area of square.

 

Here ABCD is the rectangular shape and total 9 circles are there.

Radius of the circle = 7 cm

Diameter of the circle = 14 cm

Here the circles are touched each other.  Therefore the diameter of 3 circles is equal to the side of the square.

Side of the square ABCD = 3 x diameter of circle.

                             = 3 x 14 cm = 42 cm.

Now,

          Area of the square ABCD = side²

                                                          = 42² = 1764 cm²

Hence, the area of the square is 1764 cm².

2.  Find the Area of each circular design.

Given that

                   r = 7 cm

          Area of the circle = pr²

                             =

                             = 154 cm².

Hence, area of the circle is 154 cm².

 

          (iii) Find the Area of the remaining portion of the square ABCD

In the figure the yellow shaded region is the remaining portion.  We need to find the area of the yellow shaded region.

So

          Area of the remaining portion = Area of the square – Area of 9 circles.

We already know the area of the square and the area of a circle.

Area of the square =  1764 cm²

Area of a circle =  154 cm².

Area of 9 circles = 9 x 154 = 1386 cm².

Area of the remaining part = 1764 – 1386

                                      = 378 cm².

Hence, the area of the remaining part of ABCD is 378 cm².