Pookalam is the flower bed or flower pattern designed during Onam in Kerala. It is similar as Rangoli in North India and Kolam in Tamil Nadu

 

Case Study 13

Pookalam is the flower bed or flower pattern designed during Onam in Kerala. It is similar as Rangoli in North India and Kolam in Tamil Nadu.

During the festival of Onam , your school is planning to conduct a Pookalam competition. Your friend who is a partner in competition, suggests two designs given below.

Observe these carefully

 

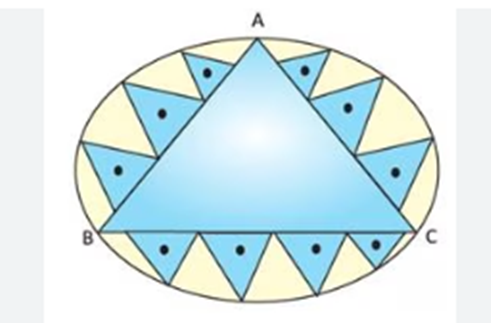
Design I: This design is made with a circle of radius 32cm leaving equilateral triangle ABC in the middle as shown in the given figure.

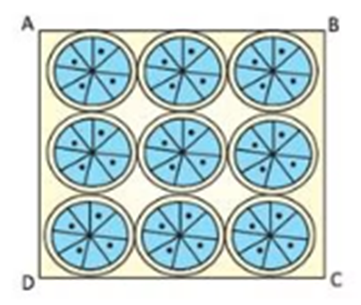
Design II: This Pookalam is made with 9 circular design each of radius 7cm.

Refer Design I:

1.  Find the side of equilateral triangle.

2.  Find the altitude of the equilateral triangle.

Refer Design II:

3.  Find the area of square.

4.  Find the Area of each circular design.

5.  Find the Area of the remaining portion of the square ABCD.

 

Solution

Refer Design I:

1.     Find the side of equilateral triangle

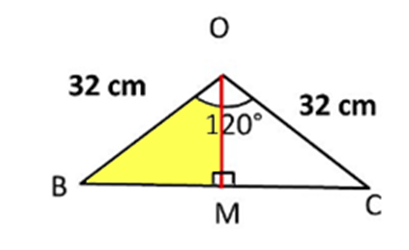
Look at the figure,

Here O is the centre of the circle

AB, BC and AC are the vertices of the triangle.

Given that D ABC is Equilateral triangle

i.e., AB = BC = AC.

Given that radius is 32 cm

i.e., OB = OC = OA = 32 cm

Now, Let us consider D OBC

Draw a line OM perpendicular to BC

i.e, OM ^ BC

Therefore, ÐOMB = 90⁰

Also

          BM = MC = ½ BC

          ÐBOM = ÐCOM = ½ ÐBOC

                             = ½ x 120

                             = 60⁰.

In right angled triangle OBM 

          Sin O =

          Sin 60⁰ =

            =

          BM =  = 16 Ö3 cm

Thus

          BC     = 2 x BM

                   = 2 x 16 Ö3

                   = 32 Ö3 cm

Hence the side of the equilateral triangle is 32 Ö3 cm.        

(ii) Find the altitude of the equilateral triangle

Draw the attitude AM perpendicular to BC

AM    = AO + OM

          =  32 + OM

Now find the OM

Consider the triangle BOM 

          Find Cos O

Cos O =

Cos 60⁰ =

½ =

OM =  cm

Therefore,

Attitude of equilateral triangle ABC = 16 + 32 = 48 cm

 

Refer Design II:

1.  Find the area of square.

 

Here ABCD is the rectangular shape and total 9 circles are there.

Radius of the circle = 7 cm

Diameter of the circle = 14 cm

Here the circles are touched each other.  Therefore the diameter of 3 circles is equal to the side of the square.

Side of the square ABCD = 3 x diameter of circle.

                             = 3 x 14 cm = 42 cm.

Now,

          Area of the square ABCD = side²

                                                          = 42² = 1764 cm²

Hence, the area of the square is 1764 cm².

2.  Find the Area of each circular design.

Given that

                   r = 7 cm

          Area of the circle = pr²

                             =

                             = 154 cm².

Hence, area of the circle is 154 cm².

 

          (iii) Find the Area of the remaining portion of the square ABCD

In the figure the yellow shaded region is the remaining portion.  We need to find the area of the yellow shaded region.

So

          Area of the remaining portion = Area of the square – Area of 9 circles.

We already know the area of the square and the area of a circle.

Area of the square =  1764 cm²

Area of a circle =  154 cm².

Area of 9 circles = 9 x 154 = 1386 cm².

Area of the remaining part = 1764 – 1386

                                      = 378 cm².

Hence, the area of the remaining part of ABCD is 378 cm².